算法设计与分析

1.递归与分治

• 分治法

  1. 分治法产生的子问题是原问题的较小规模；

  2. 反复应用分治手段，可以使子问题规模不断缩小；

  3. 最终使子问题缩小到很容易直接求出其解；

  4. 将规模较小的问题的答案逐级向上合并，可得大问题答案。

• 分治法解决问题通常使用递归算法；

• 直接或间接调用自身的算法称为递归算法。

算法中要对边界条件处理，而对非边界条件的处理要分为3步：

• 分：问题划分的子问题；
• 治：对各个子问题递归调用去解决；
• 合：合并子问题的解为问题的解。

边界条件与递归方程是递归函数的两个要素，递归函数只有具备了这两个要素，才能在有限次的计算后得到结果。

N的阶乘

int fac(int n){
    if(n==0)
        return 1;
    return n*fac(n-1);
}

斐波那契数列

int fibonacci(int n){
    if(n<=1)
        return 1;
    return fibonacci(n-1)+fibonacci(n-2);
}

全排列

#include <stdio.h>
#define Type int

void Swap(Type &a,Type &b){
 	Type temp=a;
 	a=b;
 	b=temp;
 }
 
 void Perm(Type list[],int k,int m){//产生list[k:m]元素的全排列 k,m 为数组下标
 	if(k==m){//只剩下一个元素
 		for(int i=0;i<=m;i++)
 			printf("%d ",list[i]);
 		printf("\n");
	 }
	 else{//还有多个元素待排列，递归产生排列
	 for(int i=k;i<=m;i++){
	 	Swap(list[k],list[i]);
	 	Perm(list,k+1,m);
	 	Swap(list[k],list[i]);
	 }	
	 }
 }
 
 int main(){
 	Type list[]={1,2,3};
 	Perm(list,0,2);//Perm(list,0,n-1)则产生list[0:n-1]的全排列
 	return 0;
 }

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

hanoi 塔

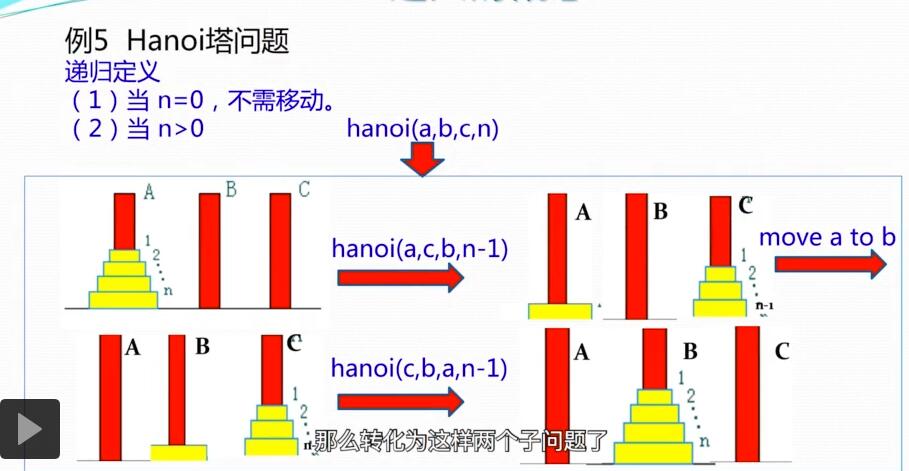
void hanoi(int n,int a,int b,int c){
	if(n>0){
		hanoi(n-1,a,c,b);//借助b柱将a移动到c
		move(a,b);
		hanoi(n-1,c,b,a);//借助a柱将c到b
 }
}

二分搜索术

int BinarySearch(ElementType A[],ElementType K,int N){//折半查找 
	int left,right,mid,Nofound=-1;
	left=0;
	right=N-1;
	while(left<=right){
		mid=(left+right)/2;
		if(K<A[mid])right=mid-1;
		else if (K>A[mid])left=mid+1;
		else return mid;
	}
	return Nofound;
}

棋盘覆盖

• 易知，在任何一个$2^k*2^k$的棋盘覆盖中，用到的 L 型骨牌个数恰为$(4^k-1)/3$

//坐标：左上行号，左上列号，特殊方格所在行号，特殊方格所在列号，棋盘大小
int tile=0;
int Board[size][size]={0};

void ChessBoard(int tr,int tc,int dr,int dc,int size){
    if(size==1)
        return;
    int t=tile++;//L型骨牌号
    int s=size/2;//分割棋盘
    //覆盖左上角子棋盘
    if(dr < tr+s && dc < tc+s) 
        ChessBoard(tr,tc,dr,dc,s);//特殊方格在此棋盘中
    else{//此棋盘中无特殊方格
        Board[tr+s-1][tc+s-1]= t ;//用 t 号 L 型骨牌覆盖右下角
        ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//覆盖其余方格
    }
    //覆盖右上角子棋盘
    if(dr<tr+s && dc >= tc+s)//特殊方格在此棋盘中
        ChessBoard(tr,tc+s,dr,dc,s);
    else{//此棋盘无特殊方格
        Board[tr+s-1][tc+s] = t;//用t号L型骨牌覆盖左下角
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s);//覆盖其余方格
    }
    //覆盖左下角子棋盘
    if(dr >= tr+s && dc < tc+s)//特殊方格在此棋盘中
        ChessBoard(tr+s,tc,dr,dc,s);
    else{//此棋盘中无特殊方格
        Board[tr+s][tr+s-1] = t;//用 t 号 L 型骨牌覆盖右上角
        ChessBoard(tr+s,tc,tr+s,tr+s-1,s);//覆盖其余方格
    }
    //覆盖右下角子棋盘
    if(dr >= tr+s && dc >= tc+s)//特殊方格在此棋盘中
        ChessBoard(tr+s,tc+s,dr,dc,s);
    else{//此棋盘中无特殊方格
        Board[tr+s][tc+s] = t;//用t号L型骨牌覆盖左上角
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s);//覆盖其余方格
    }
}

合并排序

//归并递归算法 
void Merge(ElementType A[],ElementType TmpA[],int L,int R,int RightEnd){
    int leftEnd=R-1;//左边终点位置，假设左右两列挨着 在一个数组里面
    int Tmp=L;//存放结果得数组得初始位置，从第二个数组得哪个地方开始
    int NumElements = RightEnd - L + 1;//归并结束后总元素数
    while(L<=leftEnd && R<=RightEnd){
        if(A[L]<=A[R])TmpA[Tmp++]=A[L++];
        else TmpA[Tmp++]=A[R++];
    }
    while(L<=leftEnd)
        TmpA[Tmp++]=A[L++];//直接复制左边剩下的
    while(R<=RightEnd)
        TmpA[Tmp++]=A[R++];//直接复制右边剩下得
    //两个只会执行一个
    //最后将TmpA数组倒回A数组，RightEnd 始终没变(传进来后，传进来前始终在变)
    for(int i=0;i<NumElements;i++,RightEnd--)
        A[RightEnd]=TmpA[RightEnd];
}
//分而治之 时间复杂度T(N)=T(N/2)+T(N/2)+O(N)=>T(N)=O(NlogN) 稳定
//RightEnd 始终在变 递归调用
void MSort(ElementType A[],ElementType TmpA[],int L,int RightEnd){
    int Center;
    if(L<RightEnd){
        Center = (L+RightEnd)/2;
        MSort(A,TmpA,L,Center);
        MSort(A,TmpA,Center+1,RightEnd);
        Merge(A,TmpA,L,Center+1,RightEnd);
    }
}

//统一接口 重要！！！！
void Merge_sort(ElementType A[],int N){
    ElementType *TmpA;
    TmpA=(ElementType*)malloc(N * sizeof(ElementType));
    if (TmpA!=NULL){
        MSort(A,TmpA,0,N-1);
        free(TmpA);//释放临时数组
    }
    else printf("错误");
}

//考试
//void MergeSort(Type a[],int left,int right){
//    if(left<right){//至少有2个元素
//        int i=(left+right)/2;//取中点
//        MergeSort(a,left,i);
//        MergeSort(a,i+1,right);
//        Merge(a,b,left,i,right);//合并到数组b
//        Copy(a,b,left,right);//复制回数组a
//    }
//}

void MergeSort(Type a[],int n){
    //Type *b=(Type*)malloc(n*sizeof(Type));
    Type *b = new Type [n];
    int s = 1;
    while(s<n){
        MergePass(a,b,s,n);//合并到数组b
        s +=s;
        MergePass(b,a,s,n);//合并到数组a
        s+=s;
    }
}
void mergepass(Type x[],Type y[],int s,int n){//合并大小为s的相邻子数组
    int i =0;
    while (i<=n-2*s){
        Merge(x,y,i,i+s-1,i+2*s-1);//合并大小为s的相邻2段子数组
        i=i+2*s;
    }
    if (i+s<n)						//剩下的元素个数少于2*s
        Merge(x,y,i,i+s-1,n-1);
    else
        for(int j=i;j<=n-1;j++);
    		y[j]=x[j];
}
void Merge(Type c[],Type d[],int l,int m,int r){//合并c[l:m]和c[m+1:r]到d[l:r]
    int i=l,j=m+1,k=l;
    while((i<=m) && (j<=r)){
        if(c[i]<=c[j])
            d[k++]=c[i++];
        else
            d[k++]=c[j++];
    }
        if(i>m){
            for(int q=j;q<=r;q++)
                d[k++]=c[q];
        }
        else{
            for(int q=i;q<=m;q++)
                d[k++]=c[q];
        }
}


//归并非递归算法 
void Merge1(ElementType A[],ElementType TmpA[],int L,int R,int RightEnd){
    int leftEnd=R-1;//左边终点位置，假设左右两列挨着 在一个数组里面
    int Tmp=L;//存放结果得数组得初始位置，从第二个数组得哪个地方开始
    int NumElements = RightEnd - L + 1;//归并结束后总元素数
    while(L<=leftEnd && R<=RightEnd){
        if(A[L]<=A[R])TmpA[Tmp++]=A[L++];
        else TmpA[Tmp++]=A[R++];
    }
    while(L<=leftEnd)
        TmpA[Tmp++]=A[L++];//直接复制左边剩下的
    while(R<=RightEnd)
        TmpA[Tmp++]=A[R++];//直接复制右边剩下得
    //两个只会执行一个
}

void Merge_pass(ElementType A[],ElementType TmpA[],int N,
               int length){//length = 当前有序子序列长度
    int i;
    for(i=0;i<=N-2*length;i+=2*length)
        Merge1(A,TmpA,i,i+length,i+2*length-1);//将A中元素归并到TmpA而不直接倒回来
    //处理最后两个
    if(i+length<N)//归并最后两个子列
        Merge1(A,TmpA,i,i+length,N-1);
    else//最后剩一个,直接倒进去就可以了
        for(int j=i;j<N;j++)TmpA[j]=A[j];
}

//统一接口 重要！！！！
void Merge_sort1(ElementType A[],int N){
    ElementType *TmpA;
    int length=1;
    TmpA=(ElementType*)malloc(N * sizeof(ElementType));
    if (TmpA!=NULL){
        while(length<N){
            Merge_pass(A,TmpA,N,length);
        	length *=2;
            Merge_pass(TmpA,A,N,length);
            length *=2;//两边确保最后一次将TmpA中得序列倒回 A中         
        } 
        free(TmpA);//释放临时数组
    }
    else printf("错误");
}

快速排序

void Swap(ElementType *x,ElementType *y){
    ElementType temp;
    temp = *x;
    *x=*y;
    *y=temp;
    
}
void Swap1(ElementType &x,ElementType &y){
    ElementType temp;
    temp = x;
    x=y;
    y=temp;
    
}


//快速排序     最好：O(n log2 n) 最坏：O(n^2) 平均：O(n log2 n)
ElementType Median3(ElementType A[],int Left,int Right){
    int Center=(Left+Right)/2;
    if(A[Left]>A[Center])
        //Swap(&A[Left],&A[Center]);
    	Swap1(A[Center],A[Right]);
    if(A[Left]>A[Right])
        //Swap(&A[Left],&A[Right]);
    	Swap1(A[Center],A[Right]);
    if(A[Center]>A[Right])
        //Swap(&A[Center],&A[Right]);
    	Swap1(A[Center],A[Right]);
    
    //A[Left]<=A[Center]<=A[Right]
    Swap(&A[Center],&A[Right-1]);//将pivot藏到右边倒数第二个，
    //只需考虑A[Left+1],A[Right-2]，因为第一个和最后一个已经比它小和大
    return A[Right-1];
}

void Quicksort(ElementType A[],int Left,int Right){
    if(Right-1>0 && Left+1<Right){
	int Pivot=Median3(A,Left,Right);
    int i=Left;
    int j=Right-1;
    
    for( ; ; ){
        //A[Left+1],A[Right-2]
        while(A[++i]<Pivot){}
        while(A[--j]>Pivot){}
        //两边都出现问题
        if(i<j)
            //说明都出现问题 可以调换
            Swap(&A[i],&A[j]);
        	//Swap1(A[i],A[j]);
        else break;//i>j 调换
    }
    
    Swap(&A[i],&A[Right-1]);//将Center这个数放到自己得位置上
    Quicksort(A,Left,i-1);//递归将两边集合继续划分子集排序
    Quicksort(A,i+1,Right);
	}   
}

void Quick_Sort(ElementType A[],int N){
    Quicksort(A,0,N-1);//数组下标
}

//考试快排
void Swap(Type &x,Type &y){
    int tmp=x;
    x=y;
    y=tmp;
}
void QuickSort(Type a[], int p,int r){
    if(p < r){
        int q=Partition(a,p,r);
        QuickSort(a,p,q-1); //对左半段排序
        QuickSort(a,q+1,r);//对右半段排序
    }
}

int Partition(Type a[],int p,int r){
    int i = p,j=r+1;
    Type x=a[p];
    //将小于x的元素交换到左边区域，将大于x的元素交换到右边区域
    while(true){
        while(a[++i]<x && i<r);
        while(a[--j]>x);
        if(i>=j)
            break;
        Swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(Type a[],int p,int r){
    int i=Random(p,r);
    Swap(a[i],a[p]);
    return Partition(a,p,r);
}

int RandomizedQuickSort(Type a[],int p,int r){
    if(p < r){
        int q= RandomizedPartition(a,p,r);
        RandomizedQuickSort(a,p,q-1);//对左半段排序
        RandomizedQuickSort(a,q+1,r);//对右半段排序
    }
}

线性时间选择

//采用随机快排 平均时间复杂度0(n)
Type RandomizedSelect(Type a[],int p,int r,int k){//p起点坐标 r为第n-1个位置坐标，
	if(p==r)
    	return a[p];//找到第k小元素
	int i=RandomizedPartition(a,p,r);
    int j=i-p+1;
    if(k<=j)
		return RandomizedQuickSort(a,p,i,k);//对左半段排序
    else
		return RandomizedQuickSort(a,i+1,r,k-j);//对右半段排序
}

---

2.贪心算法

活动安排

用数组f[]表示最大结束时间，并从小到大排序 s[]为其对应的开始时间,A[]辅助表示是否满足条件

template<class Type>
void GreedySelector(int n,Type s[],Type f[],bool A[]){
    sort(f,s,n);//以f[]为基准从小到大排序
    A[1]=true;
    int j=1;
    for(int i=2;i<n;i++){
        if(s[i]>=f[j]){//开始时间大于结束时间
            A[i]=true;
            j=i;         
        }else
            A[i]=false;
    }
}

void Swap(Type &x,Type &y){
    int tmp=x;
    x=y;
    y=tmp;
}
void sort(ElementType A[],ElementType B[],int N){
	for(int p=N-1;p>=0;p--){
    int flag=0;//判断是否在一趟排序过程中有序，没有触发Swap
    for(int i=0;i<p;i++){//一趟
    if(A[i]>A[i+1]){
        Swap(A[i],A[i+1]);
        Swap(B[i],B[i+1]);
        flag=1;//发生了交换
    }
    }
        if(flag==0)break;
    }
}//适合单向链表，同一顺序，稳定

最优装载

template<class Type>
void Loading(int x[],Type w[],Type c,int n){
    int *t=new int [n+1];//储存w下标
    Sort(w,t,n);//以w为基准从小到大排序，合并排序 稳定
    for(int i=1;i<=n;i++){
        x[i]=0;
    }
    for(int i=0;i<=n && w[t[i]]<=c;i++){
        x[t[i]]=1;
        c-=w[t[i]]
    }
}

哈夫曼编码

template<class Type>
class Huffman{
    friend BinaryTree<int> HuffmanTree(Type [],int);
public:
    operator Type ()const{ return weight;}
private:
    BinaryTree<int> tree;
    Type weight;
};

template<class Type>
BinaryTree<int> HuffmanTree(Type f[],int n){
    Huffman<Type> *w=new Huffman<Type> [n+1];
    BinaryTree<int> a,zero;
    for(int i=1;i<=n;i++){
        z.MakeTree(i,zero,zero);
        w[i].weight = f[i];
        w[i].tree = z;
    }
    //建优先队列
    MinHeap<Huffman<Type>>Q(1);
    Q.Initialize(w,n,n);
    //反复合并最小频率树
    Huffman<Type> x,y;
    for(int i=1;i<n;i++){
        Q.DeleteMin(x);
        Q.DeleteMin(y);
        z.MakeTree(0,x.tree,y.tree);
        w.weight+=y.weight;
        x.tree=z;
        Q.Insert(x);
    }
    Q.DeleteMin(x);
    Q.Deactivate();
    delete []w;
    return x.tree;
}

单源最短路径

针对带权有向图，设置顶点集合S,并不断地做贪心选择来扩充这个集合。

算法描述：输入一个带权有向图G=(V,E),E={1,2···,n},顶点v是源 起点。c是一个二维数组，c[i][j]表示边( i , j ) 的权。当(i,j)不属于E时，c[i][j]=∞。dist[i] 表示当前从源到顶点 i 的最短路径长度。

template<class Type>
void Dijkstra(int n,int v,Type dist[],int prev[],Type **c){
    bool s[maxint];
    for(int i=1;i<=n;i++){
        dist[i]=c[v][i];
        s[i]=false;
        if(dist[i]==maxint)
            prev[i]=0;
        else
            prev[i]=v;//当前i顶点对应的前一个顶点下标
    }
    dist[v]=0;s[v]=true;
    for(int i=1;i<n;i++){
        int temp=maxint;
        int u=v;
        for(int j=1;j<=n;j++){
            if((!s[j])&&(dist[j]<temp)){
                u=j;
                temp = dist[j];
            }
            s[u]=true;
            for(int j=1;j<=n;j++){
                if((!s[j])&&(c[u][j]<maxint)){
                    Type newdist =dist[u]+c[u][j];
                    if(newdist<dist[j]){
                        dist[j]=newdist;
                        prev[j]= u;
                    }
                }
            }
        }
    }  
}

最小生成树

//Prim
template<class Type>
Void Prim(int n,Type **c){
    Type lowcost[maxint];
    int closest[maxint];
    bool s[maxint];
    s[1]=true;
    for (int i=2;i<=n;i++){
        lowcost[i]=c[1][i];
        closest[i]=1;
        s[i]=false;
    }
    for (int i=1;i<n;i++){
        Type min=inf;
        int j=1;
        //找中使用权值最小的顶点j
        for(int k=2;k<=n;k++){
            if((lowcost[k]<min)&& (!s[k])){
                min=lowcost[k];
                j=k;
            }
        }
        //找到符合贪心选择方式的边，将顶点j加入到集合S
        cout<<j<<' '<<closest[j]<<endl;
        s[j]=true;
        
        //找到一条边后，更新数组closest和lowcost
        for(int k=2;k<=n;k++){
        	if((c[j][k]<lowcost[k]) && (!s[k])){
            	lowcost[k]=c[j][k];
                closest[k]=j;
        	}
        }
    }
}

//Kruskal
template<class Type>
class EdgeNode{
    friend ostream& operator<<(ostream&, EdgeNode<Type>);
    friend bool Kruskal(int,int ,EdgeNode<Type>*,EdgeNode<Type>*);
    friend void main(void);
public:
    operator Type ()const{return weight;}
private:
    Type weight;
    int u,v;
};

template<class Type>
bool Kruskal(int n,int e,EdgeNode<Type> E[],EdgeNode<Type> t[]){
	MinHeap<EdgeNode<Type>>H(1);
    H.Initialize(E,e,e);
    UnionFind U(n);
    int k=0;
    while (e && k< n-1){
        EdgeNode<int> x;
        H.DeletMin(x);
        e--;
        int a=U.Find(s.u);
        int b=U.Find(x.v);
        if(a!=b){
            t[k++]=x;
            U.Union(a,b);
        }
        H.Deactivate();
        return(k==n-1);
    }
}

---

3.动态规划

矩阵连乘

//计算矩阵乘积
void matrixMultiply(int **a,int **b,int **c,int ra,int ca,int rb,int cb){
    //ra,ca和rb,cb 分别表示矩阵A和B的行数和列数
    if(ca!=rb)
        error("矩阵不可乘")；
    for(int i=0;i<ra;i++){
        for(int j=0;j<cb;j++){
            int sum=a[i][0]*b[0][j];//第一个元素
            for(int k=1;k<ca;k++)
                sum+=a[i][k]*b[k][j];
            c[i][j]=sum;
        }
    }
}

//动态规划寻找最优值，输入参数存储与p中，输出最优值数组m，记录最优值断开位置数组s
void MatrixChain(int *p,int n,int **m,int **s){
    for(int i=1;i<=n;i++)
        m[i][i]=0;
    for(int r=2;r<=n;r++){
        for(int i=1;i<=n-r+1;i++){
            int j=i+r-1;
            m[i][j]=m[i+1][j]+p[i-1]*p[k]*p[j];
            s[i][j]=i;
            for(int k=i+1;k<j;k++){
                int t=m[i][k]+m[k][j]+p[i-1]*p[k]*p[j];
                if(t<m[i][j]){
                    m[i][j]=t;
                    s[i][j]=k;
                }
            }
        }
    }
}


//递归方式
void Traceback(int i,int j,int **s){
    if(i==j)
        return;
    Traceback(i,s[i][j],s);
    Traceback(s[i][j]+1,j,s);
    cout<<"Multiply A"<<i<<","<<s[i][j];
    cout<<"and A"<< (s[i][j]+1)<<","<<j<<endl;
}

最长公共子序列

void LCSlength(int m,int n,char *x,char *y,int **c,int **b){
    int i,j;
    for(i=1;i<=m;i++)
        c[i][0]=0;
    for(i=1;i<=n;i++)
        c[0][i]=0;
    for(i=1;i<=m;i++){
        for(j=1;j<=n;j++){
            if(x[i]==y[j]){//左上角
                c[i][j]=c[i-1][j-1]+1;
                b[i][j]=1;
            }
            else if(c[i-1][j] >= c[i][j-1]){//上一行
                c[i][j]=c[i-1][j];
                b[i][j]=2;
            }
            else{//前一列
                c[i][j]=c[i][j-1];
                b[i][j]=3;
            }
        }
    }
}

凸多边形最优三角剖分

template<class Type>
void MinWeightTriangulation(int n,Type **t,int **s){
    for(int i=1;i<=n;i++)
        t[i][i]=0;
    for(int r=2;r<=n;r++){
        for(int i=1;i<=n-r+1;i++){
            int j=i+r-1;
            t[i][j]=t[i+1][j]+w(i-1,i,j);
            s[i][j]=i;
            for(int k=i+1;k<i+r-1;k++){
                int u=t[i][k]+t[k+1][j]+w(i-1,k,j);
                if(u<t[i][j]){
                    t[i][j]=u;
                    s[i][j]=k;
                }
            }
        }
    }
}

最优二叉搜索树

void OBST(int a,int b,int n,int **m,int **s,int **w){
    for(int i=0;i<=n;i++){
        w[i+1][i]=a[i];
        m[i+1][i]=0;
        s[i+1][i]=0;
    }
    for(int r=0;r<n;r++){
        for(int i=1;i<=n-r;i++){
            int j=i+r,i1=s[i][j-1]>i ? s[i][j-1]:i,j1=s[i+1][j]>i ? s[i+1][j]:j
        	w[i][j]=w[i][j-1]+a[j]+b[j];
            m[i][j]=m[i][i1-1]+m[i1+1][j];
            s[i][j]=i1;
            for(int k=i1+1;k<=j1;k++){
                int t = m[i][k-1] + m[k+1][j];
                if(t<=m[i][j]){
                    m[i][j]=t;
                    s[i][j]=k;
                }
            }
        
        }
 		m[i][j] +=w[i][j];
    }
}