2层及多层神经网络的构建

发表于

1-2层神经网络

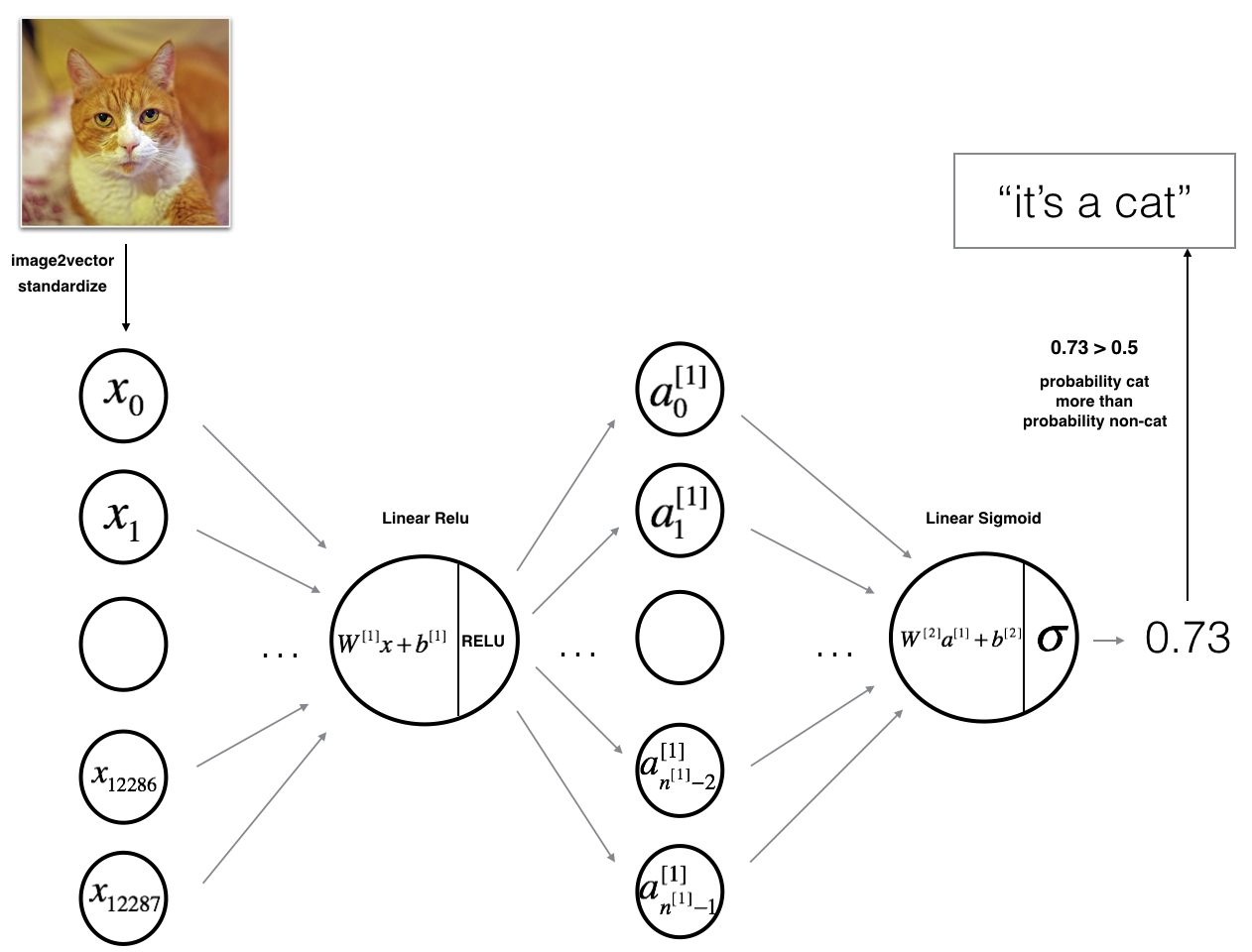
该模型可以概括为： INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT.

  • 输入是 (64,64,3) 图像，将其展平为大小为 (12288,1) 的向量。
  • 相应的向量：[x0,x1,...,x12287]T[x_0,x_1,...,x_{12287}]^T 然后乘以大小为 (n[1],12288)(n^{[1]}, 12288) 的权重矩阵 W[1]W^{[1]} 。
  • 然后，您添加一个偏差项并获取其偏倚以获得以下向量： [a0[1],a1[1],...,an[1]−1[1]]T[a_0^{[1]}, a_1^{[1]},..., a_{n^{[1]}-1}^{[1]}]^T .

    • 然后重复相同的过程。

    • 您将所得向量乘以 W[2]W^{[2]} ，然后加上截距（偏差）。

    • 最后，取最后一个激活函数为Sigmoid函数，如果大于0.5，则将其分类为猫。

步骤:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def initialize_parameters(n_x, n_h, n_y):
    ...
    return parameters 
def linear_activation_forward(A_prev, W, b, activation):
    ...
    return A, cache
def compute_cost(AL, Y):
    ...
    return cost
def linear_activation_backward(dA, cache, activation):
    ...
    return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

L层深度神经网络

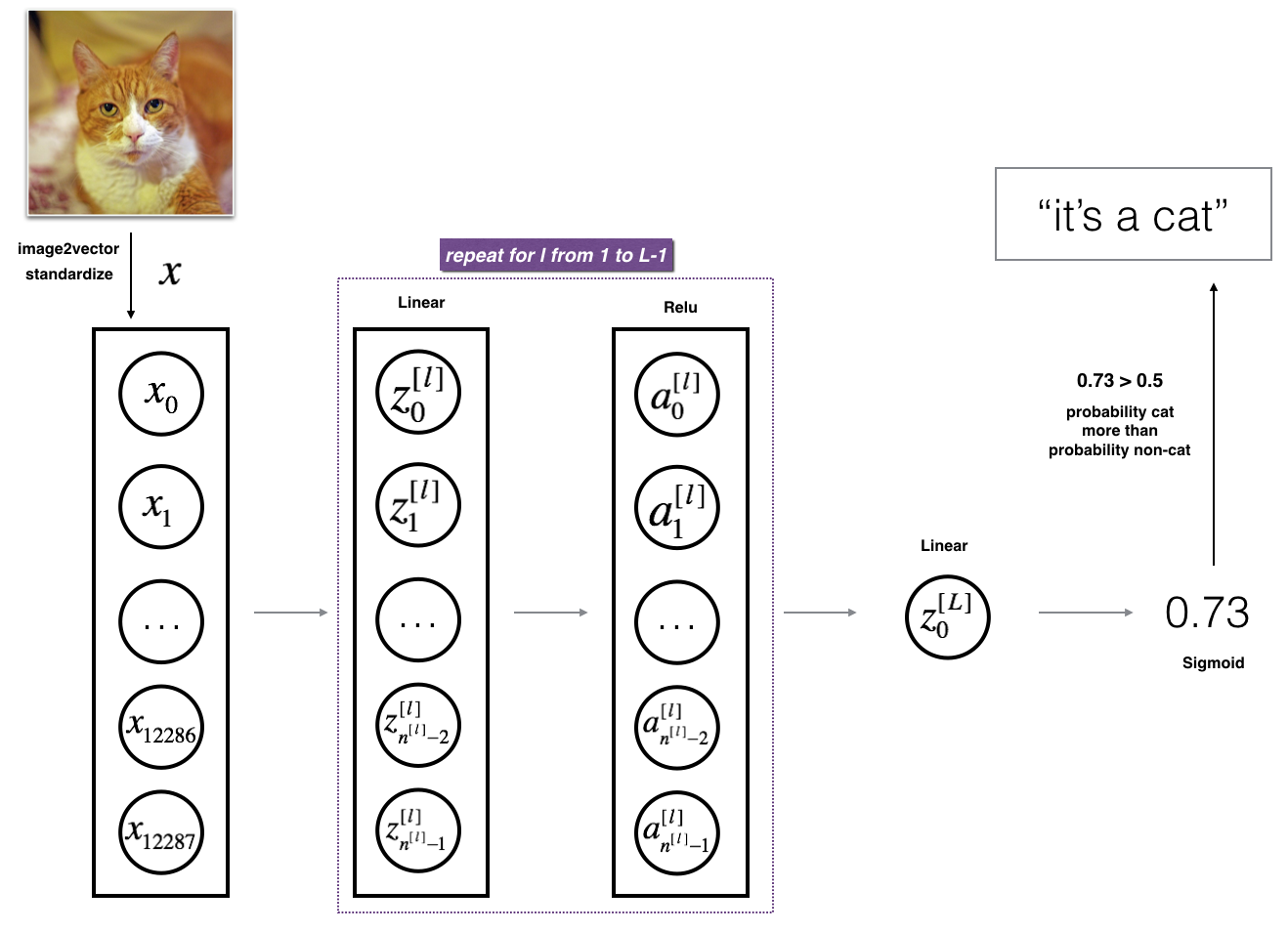
该模型可以概括为：[LINEAR -> RELU] ×\times (L-1) -> LINEAR -> SIGMOID

  • 输入是 (64,64,3) 图像，将其展平为大小为 (12288,1) 的向量。

  • 相应的向量： [x0,x1,...,x12287]T[x_0,x_1,...,x_{12287}]^T然后乘以权重矩阵W[1]W^{[1]}，然后添加截距b[1]b^{[1]},结果称为线性单位。

  • 接下来，取激活函数的ReLU，根据模型体系结构的不同，这个过程可以对每个(W[l],b[l])(W^{[l]},b^{[l]})重复多次。

  • 最后，取最后一个激活函数为Sigmoid函数。如果它大于0.5，你就把它归为猫。

步骤:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def initialize_parameters_deep(layers_dims):
    ...
    return parameters 
def L_model_forward(X, parameters):
    ...
    return AL, caches
def compute_cost(AL, Y):
    ...
    return cost
def L_model_backward(AL, Y, caches):
    ...
    return grads
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters